Prof. Dr. habil. Levente Kovács, Dr. Johanna Sápi, Dr. Dániel András Drexler
Main directions of the research
- Tumor growth model identification
- Quasi-continuous low-dosage therapy
- Optimal robust control algorithms
- Personalized treatment
A detailed description of the research
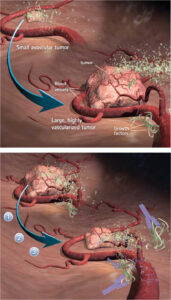
Cancer is one of the most destructive illnesses nowadays, which is lethal in most cases. According to recent statistics, 1,3 million people of the European Union are estimated to die from cancer in 2011 [1]. Unfortunately, Hungary is the leading country of the European Union (and also in the top ten in the world) in mortality data of all types of cancer [2], [3]. Conventional cytotoxic chemotherapy aims to fight directly against the tumor cells; however, it has effects on certain healthy cells of the patient as well. In addition, tumor cells can become resistant to the drug used in chemotherapy, which makes the usage of new drugs necessary. As opposed to conventional treatment, antiangiogenic therapy has limited side effects and tumor cells can not become resistant towards the angiogenic drugs. This is achieved by targeting endothelial cells instead of the tumor cells. Tumors grow uncontrolled; however, over a critical volume they can not get enough nutrients from the interstitium, so they need a vascular system for supplies achieving this by stimulating angiogenesis [4]. Antiangiogenic therapy aims to inhibit angiogenesis, but the application of the high-cost endostatin drug is based mostly on clinical expertise. Consequently, our aim was to combine the advantages of control theory with antiangiogenic therapy to optimize the treatment.
A model for tumor growth under angiogenic inhibition was presented by the Harvard Medical School and it was validated using experiments on mice with lung cancer [5]. The simplified model was presented in [6], it assumed that the tumor volume and the endothelial volume move together. Our theoretical investigations on the model proved that we can assume the administered inhibitor concentration by a simple differential equation [7]. In this way, the Dirac delta type rates, which means that the drug was given to the patient in the form of injections was changed by step function input types corresponding to infusion treatment. These assumptions were demonstrated by symbolic computations made on steady-state and dynamic analysis [8].
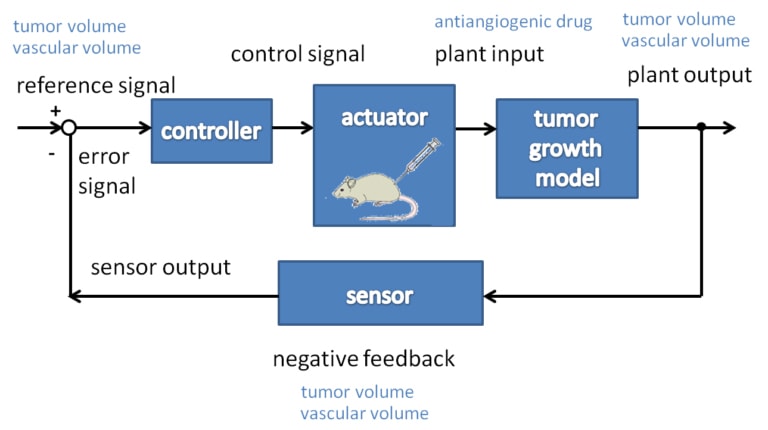
After examining the working point linearization of the nonlinear model together with linear control characteristics (observability and controllability), a Linear Quadratic (LQ) controller and an observer based on pole-placement were designed on the considered model [9].
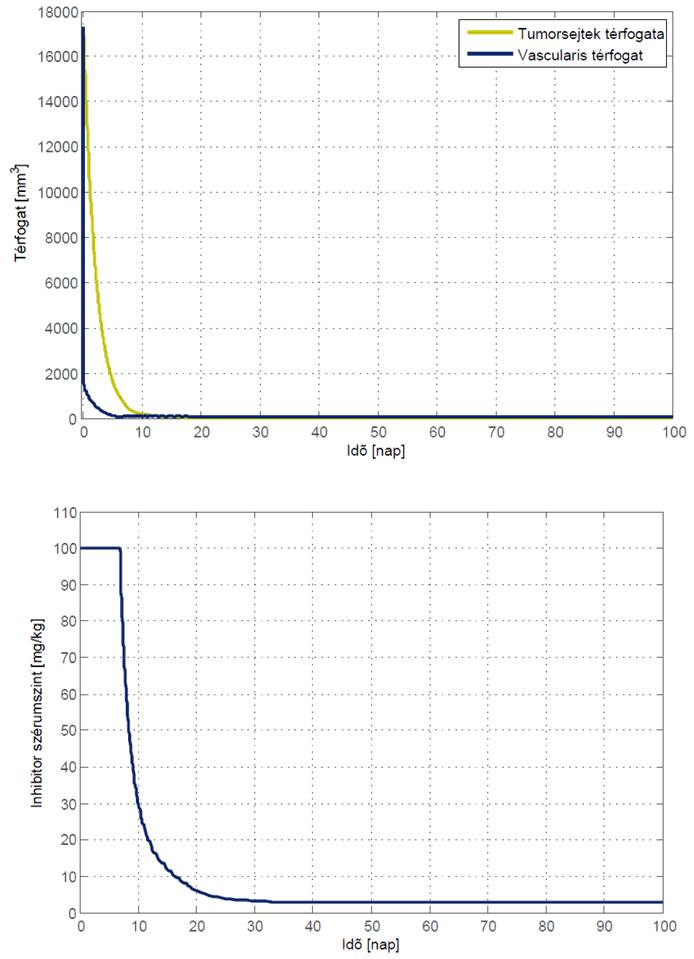
Simulation results showed that simple optimal therapy can be beneficial. Our first obtained results show that an optimal therapy could start with an intense period, where the tumor volume is compressed, followed by a maintaining period, where the minimum value of inhibitor is given to the patient.
The main significance of the controller is in the allocation of the switching time when the intense period should be terminated, and the maintaining period should be started.
Further investigations will be focused on other the application of other control strategies (nonlinear control, modern robust control) as well as on model identification, model verification and biostatistic evaluation based on mice experiments in cooperation with clinical experts.
[1] Malvezzi M., Arfé A., Bertuccio P., Levi F., La Vecchia C., Negri E.: European cancer mortality predictions for the year 2011, Annals of Oncology, 2011, doi:10.1093/annonc/mdq774.
[2] WHO, International Agency of Research on Cancer, http://www-dep.iarc.fr/.
[3] WHO, Global Health Observatory, http://www.who.int/gho/en/.
[4] A. Hoeben, B. Landuyt, M. Highley, H. Wildiers, A. T. Van Oosterom, E. A. De Bruijn, Vascular endothelial growth factor and angiogenesis, Pharmacol Rev., vol. 56, pp. 549–580, 2004.
[5] Hahnfeldt P., Panigrahy D., Folkman J., Hlatky L.: Tumor development under angiogenic signaling: A dynamical theory of tumor growth, treatment response, and postvascular dormancy, Cancer Research, 1999, Vol. 59, pp. 4770-4775.
[6] Ledzewitz U., Schatler H.: A synthesis of optimal controls for a model of tumor growth under angiogenic inhibitors, Proc. of 44th IEEE Conference on Decision and Control, and the European Control Conference, Sevilla, Spain, 2005, pp. 934-939.
[7] Drexler D. A., Harmati I., Kovács L.: Optimal control of tumor growth using antiangiogenic chemotherapy, Proc. of 3rd Int. Conf on Recent Achievements in Mechatronics, Automation, Computer Sciences and Robotics, Targu-Mures, Romania, 2011, pp. 273-284.
[8] Drexler D. A., Kovács L., Sápi J., Harmati I., Benyó Z.: Model-based analysis and synthesis of tumor growth under angiogenic inhibition: a case study, in Proc. of 18th World Congress of the International Federation of Automatic Control, Milano, Italy, 2011, pp. 3753-3758.
[9] Sápi J., Drexler D.A., Harmati I., Sápi Z., Kovács L., Linear state-feedback control synthesis of tumor growth control in antiangiogenic therapy., In: SAMI 2012 – 10th International Symposium on Applied Machine Intelligence and Informatics. Herlany, Szlovákia, 2012, pp. 143-148.