Prof. Dr. habil Levente Kovács, Dr. György Eigner, Dr. Dániel András Drexler
Main lines of research
- Nonlinear model-based robust control algorithm and LPV (Linear Parameter Varying) methodology
- Virtual patient identification using the Levenberg-Marquardt algorithm
- The framework is not sensitive to different profiles of the meal
- Hypoglycaemia can be effectively avoided
Detailed description of the research
The World Health Organization (WHO) predicts that diabetes is “the disease of the future”, especially in developing countries. The number of people with diabetes (estimated at 171 million in 2000) is projected to double by 2030 [1], [2].
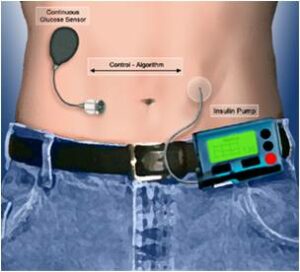
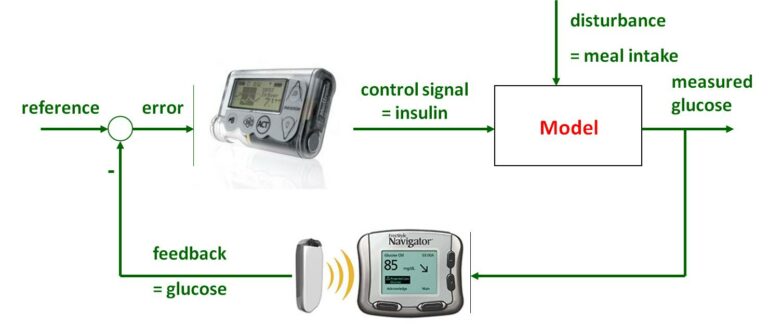
The search for an artificial pancreas can be structured in three different tasks [14]: a continuous glucose sensor for measurements, an insulin pump for infusion and a control algorithm problem.
A suitable model is needed to design a suitable control. From the many models published in the literature [4] and the wide range of control strategies [3], it is clear that modelling and controlling the behaviour of the glucose-insulin system are two closely related issues that cannot be separated. Model-predicted control has been shown to be an effective solution for the individualized management of type 1 diabetes [3], but hard constraints are also beneficial due to insulin sensitivity and patient variability [5].
Therefore, we focused on one of the most complex models, the Sorensen model [6], and developed a nonlinear model-based robust control algorithm that is more accurate compared to linear model-based methods (as it avoids linearization and directly operates on the nonlinear model itself) [7]. The nonlinear model-based approach was implemented using LPV (Linear Parameter Varying) methodology, capturing the validity of the Sorensen model in a polytopic region and building the LPV model as a linear combination of linearized models derived at each polytopic point [7].
In the context of diabetes, the Hungarian artificial pancreas research topic was briefly summarized. The developed nonlinear model-based LPV robust controller was created on the most complex Sorensen model and our first quasi-in-silico results were tested and compared with real data of 30 types of type 1 diabetes.
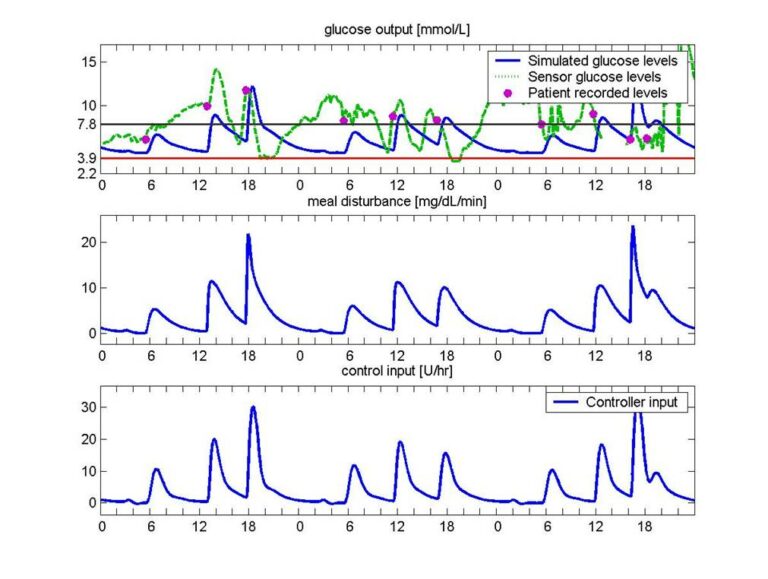
The developed framework kept blood glucose levels within the 70-120 mg/dL interval more than 90% of the time (without recalibration of the algorithm), thus demonstrating its robustness. Hypoglycaemia (caused by non-physical activity) can be effectively avoided. The research has demonstrated that there is real hope for developing a general (robust) framework that can maintain blood glucose levels within a defined interval with hard constraints; moreover, it is not sensitive to different dietary profiles. Therefore, it could effectively support individualized control (e.g. Model Predictive Control – MPC) protocols that appear in the literature [3].
Based on the results obtained, we went further and started to investigate the model-free property of the controller: if the modified Sorensen model [8] originally used is replaced by another model, how should the controller respond without being redesigned. We applied Hovorka’s well-known model [9] and created a completely new virtual patient set. This model forms the core of the University of Cambridge’s version 2.2 (SimEdu) in-silicon simulator. Using results from the Hungarian Artificial Pancreas Working Group (HAP) insulin pump centres [10], we used these two T1DM models to generate virtual patients. The identification was performed using the Levenberg-Marquardt algorithm [11] and the MATLAB Optimization toolkit. The runtime was greatly reduced by real estimation of the Jacobian matrix without the use of loops.
[1] Shaw J. E., Sicree R. A., Zimmet P. Z .: Globális becslések a cukorbetegség prevalenciájáról 2010-re és 2030-ra, 2010, Diabetes Research and Clinical Practice, vol. 87, 4–14. Oldal.
[2] Wild S., Roglic G., Green A., Sicree R., King H .: A cukorbetegség globális elterjedtsége – Becslések a 2000. évre és a 2030-ra vonatkozó előrejelzések, 2004 , Diabetes Care, Vol. 27. (5), 1047-1053. Oldal.
[3] Cobelli C., Dalla Man C., Sparacino G., Magni L., de Nicolao G., Kovatchev B .: Diabetes: modellek, jelek és Ellenőrzés (Módszertani áttekintés), IEEE Review in Biomedical Engineering, 2009, Vol. 2, 54–96. Oldal.
[4] F. Chee és F. Tyrone, Zárt hurkú vércukorszint-szabályozás, Lecture Notes of Computer Science, vol. 368, Springer-Verlag, Berlin, 2007.
[5] R. Femat, E. Ruiz-Velazquez és G. Quiroz, „Súlyozási korlátozás az intravénás inzulinszállításra a T1DM betegen H∞ Control segítségével”, IEEE tranzakciók Automation Science and Engineering, vol. 6. (2), 2009. 239-247. Oldal.
[6] J.T. Sorensen, A glükóz metabolizmusának fiziológiai modellje az emberben, és annak felhasználása a cukorbetegség javított inzulinterápiáinak tervezésére és értékelésére, PhD tézis, Dept. of Chemical Eng. Massachusettsi Műszaki Intézet, Cambridge, 1985.
[7] Kovács L., Benyó B., Bokor J. és Benyó Z. „A glükóz-inzulin rendszer indukált L2-normájának minimalizálása I. típusú cukorbetegeknél”, Számítógépes módszerek és programok a biomedicinában, vol. 102. (2), 105-118., 2011.
[8] R. S. Parker, F. J. Doyle III, J. H. Ward. és N. A. Peppas,
„Robusztus H∞ glükózkontroll cukorbetegségben fiziológiai modell alkalmazásával”, AIChE Journal, vol. 46. sz. 12, 2000. old. 2537-2549.
[9] ME Wilinska, LJ Chassin, CL Acerini, JM Allen, DB
Dunger és R. Hovorka, „Szimulációs környezet a zárt hurkú inzulinadagoló rendszerek értékeléséhez típusú cukorbetegség ”, J Diabetes Sci Technol, vol. 4. sz. 1, 2010. p. 132–144.
[10] Kovács L., Barkai L .: Magyar Mesterséges Hasnyálmirigy Műhely, Diabetologia Hungarica, 2010, Vol. XXVIII (4), 336-337. Oldal.
[11] J. Nocedal és S. J. Wright, Numerical Optimization, Springer,
Heidelberg; 2006.